Tidymodels

Math 150 - Spring 2023

Author

Jo Hardin (from Mine Çetinkaya-Rundel)

Agenda

Workflow to help us think about model building
Breaking up data for independent assessment
Assessment metrics

Comparing Models

Data Modeling: The analysis in this culture starts with assuming a stochastic data model for the inside of the black box…The values of the parameters are estimated from the data and the model then used for information and/or prediction
Algorithmic Modeling: The analysis in this culture considers the inside of the box complex and unknown. The approach is to find a function f(x) — an algorithm that operates on x to predict the responses y.

Reference: Leo Breiman (2001)

Data & goal

Data: Project FeederWatch#TidyTuesday dataset on Project FeederWatch, a citizen science project for bird science, by way of TidyTuesday.
Can the characteristics of the bird feeder site like the surrounding yard and habitat predict whether a bird feeder site will be used by squirrels?

Rows: 235,685
Columns: 59
$ squirrels                    <fct> no squirrels, no squirrels, no squirrels,…
$ yard_type_pavement           <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…
$ yard_type_garden             <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…
$ yard_type_landsca            <dbl> 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 1, 1, 1, 1,…
$ yard_type_woods              <dbl> 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1,…
$ yard_type_desert             <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…
$ hab_dcid_woods               <dbl> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, NA, NA, NA,…
$ hab_evgr_woods               <dbl> NA, NA, NA, NA, 0, 0, NA, NA, NA, NA, NA,…
$ hab_mixed_woods              <dbl> 1, 1, 1, 1, 1, 1, NA, NA, NA, NA, 1, 1, 1…
$ hab_orchard                  <dbl> NA, NA, NA, NA, 0, 0, NA, NA, NA, NA, NA,…
$ hab_park                     <dbl> NA, NA, NA, NA, 0, 0, NA, NA, NA, NA, 1, …
$ hab_water_fresh              <dbl> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,…
$ hab_water_salt               <dbl> NA, NA, NA, NA, 0, 0, NA, NA, NA, NA, 1, …
$ hab_residential              <dbl> 1, 1, 1, 1, 1, 1, NA, NA, NA, NA, 1, 1, 1…
$ hab_industrial               <dbl> NA, NA, NA, NA, 0, 0, NA, NA, NA, NA, 1, …
$ hab_agricultural             <dbl> 1, 1, 1, 1, 1, 1, NA, NA, NA, NA, 1, 1, 1…
$ hab_desert_scrub             <dbl> NA, NA, NA, NA, 0, 0, NA, NA, NA, NA, NA,…
$ hab_young_woods              <dbl> NA, NA, NA, NA, 0, 0, NA, NA, NA, NA, NA,…
$ hab_swamp                    <dbl> NA, NA, NA, NA, 0, 0, NA, NA, NA, NA, NA,…
$ hab_marsh                    <dbl> 1, 1, 1, 1, 1, 1, NA, NA, NA, NA, 1, 1, 1…
$ evgr_trees_atleast           <dbl> 11, 11, 11, 11, 11, 11, 0, 0, 0, 4, 1, 1,…
$ evgr_shrbs_atleast           <dbl> 4, 4, 4, 4, 1, 1, 1, 1, 1, 1, 4, 4, 4, 4,…
$ dcid_trees_atleast           <dbl> 11, 11, 11, 11, 1, 1, 11, 11, 11, 11, 4, …
$ dcid_shrbs_atleast           <dbl> 4, 4, 4, 4, 4, 4, 11, 11, 11, 11, 4, 4, 4…
$ fru_trees_atleast            <dbl> 4, 4, 4, 4, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,…
$ cacti_atleast                <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…
$ brsh_piles_atleast           <dbl> 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1,…
$ water_srcs_atleast           <dbl> 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0,…
$ bird_baths_atleast           <dbl> 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 1,…
$ nearby_feeders               <dbl> 0, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 1,…
$ cats                         <dbl> 0, 1, 1, 1, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1,…
$ dogs                         <dbl> 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 1,…
$ humans                       <dbl> 0, 0, 0, 0, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1,…
$ housing_density              <dbl> 2, 2, 2, 2, 2, 2, 1, 1, 1, 1, 2, 2, 2, 2,…
$ fed_in_jan                   <dbl> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, NA, 1, N…
$ fed_in_feb                   <dbl> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, NA, 1, N…
$ fed_in_mar                   <dbl> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, NA, 1, N…
$ fed_in_apr                   <dbl> 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, NA, 0, N…
$ fed_in_may                   <dbl> 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, NA, 0, N…
$ fed_in_jun                   <dbl> 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, NA, 0, N…
$ fed_in_jul                   <dbl> 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, NA, 0, N…
$ fed_in_aug                   <dbl> 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, NA, 0, N…
$ fed_in_sep                   <dbl> 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, NA, 0, N…
$ fed_in_oct                   <dbl> 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, NA, 1, N…
$ fed_in_nov                   <dbl> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, NA, 1, N…
$ fed_in_dec                   <dbl> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, NA, 1, N…
$ numfeeders_suet              <dbl> 1, 1, 1, 1, 1, 1, 3, 3, 3, 3, 1, 1, 1, 2,…
$ numfeeders_ground            <dbl> NA, 0, 0, 0, NA, NA, 1, 1, 1, 1, 3, 3, 3,…
$ numfeeders_hanging           <dbl> 1, 1, 1, 3, NA, NA, 2, 2, 2, 2, 2, 2, 1, …
$ numfeeders_platfrm           <dbl> 1, 1, 1, 0, NA, NA, 1, 1, 1, 2, 1, 1, 1, …
$ numfeeders_humming           <dbl> NA, 0, 0, 0, NA, NA, 1, 1, 1, 1, NA, 0, 0…
$ numfeeders_water             <dbl> 1, 1, 1, 1, NA, NA, 2, 2, 2, 2, 1, 1, 1, …
$ numfeeders_thistle           <dbl> NA, 0, 0, 0, NA, NA, 1, 1, 1, 2, 1, 1, 1,…
$ numfeeders_fruit             <dbl> NA, 0, 0, 0, NA, NA, 1, 1, 1, 1, NA, 0, 0…
$ numfeeders_hopper            <dbl> NA, NA, NA, NA, 1, 1, NA, NA, NA, NA, NA,…
$ numfeeders_tube              <dbl> NA, NA, NA, NA, 1, 1, NA, NA, NA, NA, NA,…
$ numfeeders_other             <dbl> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, N…
$ population_atleast           <dbl> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 5001, 5001,…
$ count_area_size_sq_m_atleast <dbl> 1.01, 1.01, 1.01, 1.01, 1.01, 1.01, 375.0…

Feeders

How are other characteristics related to the presence of squirrels?

# A tibble: 2 × 2
  squirrels    nearby_feeders
  <fct>                 <dbl>
1 no squirrels          0.344
2 squirrels             0.456

Other variables

What about some of the variables describing the habitat?

Modeling

Train / test

Create an initial split:

set.seed(470)
feeder_split <- site_data %>%
  initial_split(strata = squirrels) # prop = 3/4 in each group, by default

Save training data

feeder_train <- training(feeder_split)
dim(feeder_train)

[1] 176763     59

Save testing data

feeder_test  <- testing(feeder_split)
dim(feeder_test)

[1] 58922    59

Training data

feeder_train

# A tibble: 176,763 × 59
   squirrels    yard_t…¹ yard_…² yard_…³ yard_…⁴ yard_…⁵ hab_d…⁶ hab_e…⁷ hab_m…⁸
   <fct>           <dbl>   <dbl>   <dbl>   <dbl>   <dbl>   <dbl>   <dbl>   <dbl>
 1 no squirrels        0       0       1       0       0       1      NA       1
 2 no squirrels        0       0       1       0       0       1      NA       1
 3 no squirrels        0       0       1       0       0       1       0       1
 4 no squirrels        0       0       1       0       0       1      NA      NA
 5 no squirrels        0       0       1       1       0       1       0       0
 6 no squirrels        0       0       1       0       0       1      NA       1
 7 no squirrels        0       0       0       1       0       0       0       1
 8 no squirrels        0       0       1       1       0      NA      NA      NA
 9 no squirrels        0       0       1       0       0       1       1      NA
10 no squirrels        0       0       1       1       0       0       0       1
# … with 176,753 more rows, 50 more variables: hab_orchard <dbl>,
#   hab_park <dbl>, hab_water_fresh <dbl>, hab_water_salt <dbl>,
#   hab_residential <dbl>, hab_industrial <dbl>, hab_agricultural <dbl>,
#   hab_desert_scrub <dbl>, hab_young_woods <dbl>, hab_swamp <dbl>,
#   hab_marsh <dbl>, evgr_trees_atleast <dbl>, evgr_shrbs_atleast <dbl>,
#   dcid_trees_atleast <dbl>, dcid_shrbs_atleast <dbl>,
#   fru_trees_atleast <dbl>, cacti_atleast <dbl>, brsh_piles_atleast <dbl>, …

Feature engineering

We prefer simple models when possible, but parsimony does not mean sacrificing accuracy (or predictive performance) in the interest of simplicity
Variables that go into the model and how they are represented are just as critical to success of the model
Feature engineering allows us to get creative with our predictors in an effort to make them more useful for our model (to increase its predictive performance)

Modeling workflow

Create a recipe for feature engineering steps to be applied to the training data
Fit the model to the training data after these steps have been applied
Using the model estimates from the training data, predict outcomes for the test data
Evaluate the performance of the model on the test data

Building recipes

Initiate a recipe

feeder_rec <- recipe(
  squirrels ~ .,    # formula
  data = feeder_train 
  )

feeder_rec

Recipe

Inputs:

      role #variables
   outcome          1
 predictor         58

Working with recipes

When building recipes you in a pipeline, you don’t get to see the effect of the recipe on your data, which can be unsettling
You can take a peek at what will happen when you ultimately apply the recipe to your data at the time of fitting the model
This requires two functions: prep() to train the recipe and bake() to apply it to your data

. . .

Note

Using prep() and bake() are shown here for demonstrative purposes. They do not need to be a part of your pipeline. I do find them assuring, however, so that I can see the effects of the recipe steps as the recipe is built.

Impute missing values & Remove zero variance predictors

Impute missing values (replace with mean).
Remove all predictors that contain only a single value

feeder_rec <- feeder_rec %>%
  step_impute_mean(all_numeric_predictors()) %>%
  step_nzv(all_numeric_predictors())

feeder_rec

Recipe

Inputs:

      role #variables
   outcome          1
 predictor         58

Operations:

Mean imputation for all_numeric_predictors()
Sparse, unbalanced variable filter on all_numeric_predictors()

Prep and bake

feeder_rec_trained <- prep(feeder_rec)

bake(feeder_rec_trained, feeder_train) %>%
  glimpse()

Rows: 176,763
Columns: 59
$ yard_type_pavement           <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…
$ yard_type_garden             <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…
$ yard_type_landsca            <dbl> 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1,…
$ yard_type_woods              <dbl> 0, 0, 0, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1, 0,…
$ yard_type_desert             <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…
$ hab_dcid_woods               <dbl> 1.0000000, 1.0000000, 1.0000000, 1.000000…
$ hab_evgr_woods               <dbl> 0.223341, 0.223341, 0.000000, 0.223341, 0…
$ hab_mixed_woods              <dbl> 1.000000, 1.000000, 1.000000, 0.655411, 0…
$ hab_orchard                  <dbl> 0.09324933, 0.09324933, 0.00000000, 0.093…
$ hab_park                     <dbl> 0.4502185, 0.4502185, 0.0000000, 0.450218…
$ hab_water_fresh              <dbl> 1.0000000, 1.0000000, 1.0000000, 1.000000…
$ hab_water_salt               <dbl> 0.05016023, 0.05016023, 0.00000000, 0.050…
$ hab_residential              <dbl> 1.0000000, 1.0000000, 1.0000000, 1.000000…
$ hab_industrial               <dbl> 0.2215792, 0.2215792, 0.0000000, 0.221579…
$ hab_agricultural             <dbl> 1.0000000, 1.0000000, 1.0000000, 0.409835…
$ hab_desert_scrub             <dbl> 0.09257371, 0.09257371, 0.00000000, 0.092…
$ hab_young_woods              <dbl> 0.349782, 0.349782, 0.000000, 0.349782, 0…
$ hab_swamp                    <dbl> 0.2917369, 0.2917369, 0.0000000, 0.291736…
$ hab_marsh                    <dbl> 1.0000000, 1.0000000, 1.0000000, 0.175361…
$ evgr_trees_atleast           <dbl> 11, 11, 11, 0, 11, 1, 4, 4, 4, 1, 1, 1, 1…
$ evgr_shrbs_atleast           <dbl> 4, 4, 1, 4, 0, 1, 4, 4, 4, 1, 0, 4, 4, 11…
$ dcid_trees_atleast           <dbl> 11, 11, 1, 4, 1, 4, 11, 11, 4, 1, 1, 1, 1…
$ dcid_shrbs_atleast           <dbl> 4, 4, 4, 1, 1, 4, 11, 11, 1, 1, 0, 4, 4, …
$ fru_trees_atleast            <dbl> 4.00000, 4.00000, 1.00000, 1.00000, 0.000…
$ cacti_atleast                <dbl> 0.0000000, 0.0000000, 0.0000000, 0.000000…
$ brsh_piles_atleast           <dbl> 0, 0, 0, 1, 0, 0, 1, 4, 1, 0, 0, 1, 1, 1,…
$ water_srcs_atleast           <dbl> 1.0000000, 1.0000000, 1.0000000, 0.000000…
$ bird_baths_atleast           <dbl> 0, 0, 0, 1, 0, 0, 1, 1, 4, 0, 0, 0, 0, 1,…
$ nearby_feeders               <dbl> 1, 1, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 1,…
$ cats                         <dbl> 1, 1, 1, 1, 0, 0, 0, 1, 0, 1, 1, 0, 0, 0,…
$ dogs                         <dbl> 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 1, 1, 0, 1,…
$ humans                       <dbl> 0, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1,…
$ housing_density              <dbl> 2, 2, 2, 2, 2, 3, 1, 1, 1, 1, 2, 1, 2, 2,…
$ fed_in_jan                   <dbl> 1.0000000, 1.0000000, 1.0000000, 1.000000…
$ fed_in_feb                   <dbl> 1.000000, 1.000000, 1.000000, 1.000000, 1…
$ fed_in_mar                   <dbl> 1.0000000, 1.0000000, 1.0000000, 1.000000…
$ fed_in_apr                   <dbl> 1.0000000, 1.0000000, 0.0000000, 1.000000…
$ fed_in_may                   <dbl> 0.0000000, 0.0000000, 0.0000000, 1.000000…
$ fed_in_jun                   <dbl> 0.0000000, 0.0000000, 0.0000000, 1.000000…
$ fed_in_jul                   <dbl> 0.000000, 0.000000, 0.000000, 1.000000, 1…
$ fed_in_aug                   <dbl> 0.0000000, 0.0000000, 0.0000000, 1.000000…
$ fed_in_sep                   <dbl> 0.0000000, 0.0000000, 0.0000000, 1.000000…
$ fed_in_oct                   <dbl> 0.0000000, 0.0000000, 0.0000000, 1.000000…
$ fed_in_nov                   <dbl> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,…
$ fed_in_dec                   <dbl> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,…
$ numfeeders_suet              <dbl> 1, 1, 1, 2, 1, 1, 1, 1, 3, 2, 2, 3, 4, 1,…
$ numfeeders_ground            <dbl> 0.000000, 0.000000, 1.270686, 1.000000, 0…
$ numfeeders_hanging           <dbl> 1.000000, 1.000000, 2.707598, 2.000000, 2…
$ numfeeders_platfrm           <dbl> 1.000000, 1.000000, 1.033629, 1.033629, 0…
$ numfeeders_humming           <dbl> 0.0000000, 0.0000000, 0.4989854, 0.498985…
$ numfeeders_water             <dbl> 1.0000000, 1.0000000, 0.7887147, 0.788714…
$ numfeeders_thistle           <dbl> 0.000000, 0.000000, 1.007624, 1.000000, 1…
$ numfeeders_fruit             <dbl> 0.0000000, 0.0000000, 0.1442454, 0.144245…
$ numfeeders_hopper            <dbl> 1.385205, 1.385205, 1.000000, 1.385205, 0…
$ numfeeders_tube              <dbl> 2.162308, 2.162308, 1.000000, 2.162308, 2…
$ numfeeders_other             <dbl> 0.6037683, 0.6037683, 0.6037683, 0.603768…
$ population_atleast           <dbl> 1, 1, 1, 25001, 5001, 25001, 1, 1, 1, 1, …
$ count_area_size_sq_m_atleast <dbl> 1.01, 1.01, 1.01, 1.01, 1.01, 1.01, 375.0…
$ squirrels                    <fct> no squirrels, no squirrels, no squirrels,…

Building workflows

Specify model

feeder_log <- logistic_reg() %>%
  set_engine("glm")

feeder_log

Logistic Regression Model Specification (classification)

Computational engine: glm

Build workflow

Workflows bring together models and recipes so that they can be easily applied to both the training and test data.

feeder_wflow <- workflow() %>%
  add_recipe(feeder_rec) %>%
  add_model(feeder_log)

See next slide for workflow…

View workflow

feeder_wflow

══ Workflow ════════════════════════════════════════════════════════════════════
Preprocessor: Recipe
Model: logistic_reg()

── Preprocessor ────────────────────────────────────────────────────────────────
2 Recipe Steps

• step_impute_mean()
• step_nzv()

── Model ───────────────────────────────────────────────────────────────────────
Logistic Regression Model Specification (classification)

Computational engine: glm

Fit model to training data

feeder_fit <- feeder_wflow %>%
  fit(data = feeder_train)

feeder_fit %>% tidy()

# A tibble: 59 × 5
   term               estimate std.error statistic   p.value
   <chr>                 <dbl>     <dbl>     <dbl>     <dbl>
 1 (Intercept)         -1.42      0.0505    -28.2  2.26e-174
 2 yard_type_pavement  -0.854     0.149      -5.74 9.23e-  9
 3 yard_type_garden    -0.175     0.0392     -4.47 7.89e-  6
 4 yard_type_landsca    0.168     0.0219      7.69 1.45e- 14
 5 yard_type_woods      0.309     0.0170     18.1  1.59e- 73
 6 yard_type_desert    -0.297     0.0789     -3.76 1.68e-  4
 7 hab_dcid_woods       0.336     0.0161     20.9  6.55e- 97
 8 hab_evgr_woods      -0.0797    0.0192     -4.15 3.36e-  5
 9 hab_mixed_woods      0.420     0.0158     26.5  3.17e-155
10 hab_orchard         -0.307     0.0252    -12.2  4.00e- 34
# … with 49 more rows

. . .

So many predictors!

Model fit summary

feeder_fit %>% tidy()

# A tibble: 59 × 5
   term               estimate std.error statistic   p.value
   <chr>                 <dbl>     <dbl>     <dbl>     <dbl>
 1 (Intercept)         -1.42      0.0505    -28.2  2.26e-174
 2 yard_type_pavement  -0.854     0.149      -5.74 9.23e-  9
 3 yard_type_garden    -0.175     0.0392     -4.47 7.89e-  6
 4 yard_type_landsca    0.168     0.0219      7.69 1.45e- 14
 5 yard_type_woods      0.309     0.0170     18.1  1.59e- 73
 6 yard_type_desert    -0.297     0.0789     -3.76 1.68e-  4
 7 hab_dcid_woods       0.336     0.0161     20.9  6.55e- 97
 8 hab_evgr_woods      -0.0797    0.0192     -4.15 3.36e-  5
 9 hab_mixed_woods      0.420     0.0158     26.5  3.17e-155
10 hab_orchard         -0.307     0.0252    -12.2  4.00e- 34
# … with 49 more rows

All together

feeder_rec <- recipe(
  squirrels ~ .,    # formula
  data = feeder_train 
  ) %>%
  step_impute_mean(all_numeric_predictors()) %>%
  step_nzv(all_numeric_predictors())

feeder_rec

Recipe

Inputs:

      role #variables
   outcome          1
 predictor         58

Operations:

Mean imputation for all_numeric_predictors()
Sparse, unbalanced variable filter on all_numeric_predictors()

feeder_log <- logistic_reg() %>%
  set_engine("glm")

feeder_log

Logistic Regression Model Specification (classification)

Computational engine: glm

feeder_wflow <- workflow() %>%
  add_recipe(feeder_rec) %>%
  add_model(feeder_log) 
feeder_wflow

══ Workflow ════════════════════════════════════════════════════════════════════
Preprocessor: Recipe
Model: logistic_reg()

── Preprocessor ────────────────────────────────────────────────────────────────
2 Recipe Steps

• step_impute_mean()
• step_nzv()

── Model ───────────────────────────────────────────────────────────────────────
Logistic Regression Model Specification (classification)

Computational engine: glm

feeder_fit <- feeder_wflow %>%
  fit(data = feeder_train)

feeder_fit %>% tidy()

# A tibble: 59 × 5
   term               estimate std.error statistic   p.value
   <chr>                 <dbl>     <dbl>     <dbl>     <dbl>
 1 (Intercept)         -1.42      0.0505    -28.2  2.26e-174
 2 yard_type_pavement  -0.854     0.149      -5.74 9.23e-  9
 3 yard_type_garden    -0.175     0.0392     -4.47 7.89e-  6
 4 yard_type_landsca    0.168     0.0219      7.69 1.45e- 14
 5 yard_type_woods      0.309     0.0170     18.1  1.59e- 73
 6 yard_type_desert    -0.297     0.0789     -3.76 1.68e-  4
 7 hab_dcid_woods       0.336     0.0161     20.9  6.55e- 97
 8 hab_evgr_woods      -0.0797    0.0192     -4.15 3.36e-  5
 9 hab_mixed_woods      0.420     0.0158     26.5  3.17e-155
10 hab_orchard         -0.307     0.0252    -12.2  4.00e- 34
# … with 49 more rows

feeder_train_pred <- predict(feeder_fit, feeder_train, type = "prob") %>%
  mutate(.pred_class = as.factor(ifelse(.pred_squirrels >=0.5,
                                        "squirrels", "no squirrels"))) %>%
  bind_cols(feeder_train %>% select(squirrels))

feeder_train_pred

# A tibble: 176,763 × 4
   `.pred_no squirrels` .pred_squirrels .pred_class squirrels   
                  <dbl>           <dbl> <fct>       <fct>       
 1                0.168           0.832 squirrels   no squirrels
 2                0.168           0.832 squirrels   no squirrels
 3                0.358           0.642 squirrels   no squirrels
 4                0.166           0.834 squirrels   no squirrels
 5                0.274           0.726 squirrels   no squirrels
 6                0.191           0.809 squirrels   no squirrels
 7                0.288           0.712 squirrels   no squirrels
 8                0.184           0.816 squirrels   no squirrels
 9                0.227           0.773 squirrels   no squirrels
10                0.350           0.650 squirrels   no squirrels
# … with 176,753 more rows

Evaluate model

sensitivty = number of squirrels that are accurately predicted to be squirrels (true positive rate)

specificity = number of non-squirrels that are accurately predicted to be non-squirrels (true negative rate)

Make predictions for training data

feeder_train_pred <- predict(feeder_fit, feeder_train, type = "prob") %>%
  mutate(.pred_class = as.factor(ifelse(.pred_squirrels >=0.5,
                                        "squirrels", "no squirrels"))) %>%
  bind_cols(feeder_train %>% select(squirrels))

feeder_train_pred

# A tibble: 176,763 × 4
   `.pred_no squirrels` .pred_squirrels .pred_class squirrels   
                  <dbl>           <dbl> <fct>       <fct>       
 1                0.168           0.832 squirrels   no squirrels
 2                0.168           0.832 squirrels   no squirrels
 3                0.358           0.642 squirrels   no squirrels
 4                0.166           0.834 squirrels   no squirrels
 5                0.274           0.726 squirrels   no squirrels
 6                0.191           0.809 squirrels   no squirrels
 7                0.288           0.712 squirrels   no squirrels
 8                0.184           0.816 squirrels   no squirrels
 9                0.227           0.773 squirrels   no squirrels
10                0.350           0.650 squirrels   no squirrels
# … with 176,753 more rows

Accuracy

rbind(accuracy(feeder_train_pred, truth = squirrels, 
               estimate = .pred_class),
      sensitivity(feeder_train_pred, truth = squirrels, 
                  estimate = .pred_class, event_level = "second"),
      specificity(feeder_train_pred, truth = squirrels, 
                  estimate = .pred_class, event_level = "second"))

# A tibble: 3 × 3
  .metric     .estimator .estimate
  <chr>       <chr>          <dbl>
1 accuracy    binary         0.815
2 sensitivity binary         0.985
3 specificity binary         0.101

Visualizing accuracy

feeder_train_pred %>%
  select(squirrels, .pred_class) %>%
  yardstick::conf_mat(squirrels, .pred_class) %>%
  autoplot(type = "heatmap") + 
  scale_fill_gradient(low="#D6EAF8", high="#2E86C1")

. . .

But, really…

who cares about predictions on training data?

Make predictions for testing data

feeder_test_pred <- predict(feeder_fit, feeder_test, type = "prob") %>%
  mutate(.pred_class = as.factor(ifelse(.pred_squirrels >=0.5,
                                        "squirrels", "no squirrels"))) %>%
  bind_cols(feeder_test %>% select(squirrels))

feeder_test_pred

# A tibble: 58,922 × 4
   `.pred_no squirrels` .pred_squirrels .pred_class squirrels   
                  <dbl>           <dbl> <fct>       <fct>       
 1               0.201            0.799 squirrels   no squirrels
 2               0.156            0.844 squirrels   no squirrels
 3               0.352            0.648 squirrels   no squirrels
 4               0.197            0.803 squirrels   squirrels   
 5               0.121            0.879 squirrels   squirrels   
 6               0.272            0.728 squirrels   squirrels   
 7               0.0459           0.954 squirrels   squirrels   
 8               0.0341           0.966 squirrels   squirrels   
 9               0.0631           0.937 squirrels   squirrels   
10               0.0312           0.969 squirrels   squirrels   
# … with 58,912 more rows

Evaluate testing data

rbind(accuracy(feeder_test_pred, truth = squirrels, 
               estimate = .pred_class),
      sensitivity(feeder_test_pred, truth = squirrels, 
                  estimate = .pred_class, event_level = "second"),
      specificity(feeder_test_pred, truth = squirrels, 
                  estimate = .pred_class, event_level = "second"))

# A tibble: 3 × 3
  .metric     .estimator .estimate
  <chr>       <chr>          <dbl>
1 accuracy    binary        0.814 
2 sensitivity binary        0.985 
3 specificity binary        0.0988

Evaluate testing data

feeder_test_pred %>%
  select(squirrels, .pred_class) %>%
  yardstick::conf_mat(squirrels, .pred_class) %>%
  autoplot(type = "heatmap") + 
  scale_fill_gradient(low="#D6EAF8", high="#2E86C1")

Training vs. testing

# A tibble: 3 × 3
  .metric     .estimator .estimate
  <chr>       <chr>          <dbl>
1 accuracy    binary         0.815
2 sensitivity binary         0.985
3 specificity binary         0.101

# A tibble: 3 × 3
  .metric     .estimator .estimate
  <chr>       <chr>          <dbl>
1 accuracy    binary        0.814 
2 sensitivity binary        0.985 
3 specificity binary        0.0988

What’s up with training data?

The training set does not have the capacity to be a good arbiter of performance.
It is not an independent piece of information; predicting the training set can only reflect what the model already knows.
Suppose you give a class a test, then give them the answers, then provide the same test. The student scores on the second test do not accurately reflect what they know about the subject; these scores would probably be higher than their results on the first test.

All together

feeder_rec <- recipe(
  squirrels ~ .,    # formula
  data = feeder_train 
  ) %>%
  step_impute_mean(all_numeric_predictors()) %>%
  step_nzv(all_numeric_predictors())

feeder_rec

Recipe

Inputs:

      role #variables
   outcome          1
 predictor         58

Operations:

Mean imputation for all_numeric_predictors()
Sparse, unbalanced variable filter on all_numeric_predictors()

feeder_log <- logistic_reg() %>%
  set_engine("glm")

feeder_log

Logistic Regression Model Specification (classification)

Computational engine: glm

feeder_wflow <- workflow() %>%
  add_recipe(feeder_rec) %>%
  add_model(feeder_log) 

feeder_wflow

══ Workflow ════════════════════════════════════════════════════════════════════
Preprocessor: Recipe
Model: logistic_reg()

── Preprocessor ────────────────────────────────────────────────────────────────
2 Recipe Steps

• step_impute_mean()
• step_nzv()

── Model ───────────────────────────────────────────────────────────────────────
Logistic Regression Model Specification (classification)

Computational engine: glm

feeder_fit <- feeder_wflow %>%
  fit(data = feeder_train)

feeder_fit %>% tidy()

# A tibble: 59 × 5
   term               estimate std.error statistic   p.value
   <chr>                 <dbl>     <dbl>     <dbl>     <dbl>
 1 (Intercept)         -1.42      0.0505    -28.2  2.26e-174
 2 yard_type_pavement  -0.854     0.149      -5.74 9.23e-  9
 3 yard_type_garden    -0.175     0.0392     -4.47 7.89e-  6
 4 yard_type_landsca    0.168     0.0219      7.69 1.45e- 14
 5 yard_type_woods      0.309     0.0170     18.1  1.59e- 73
 6 yard_type_desert    -0.297     0.0789     -3.76 1.68e-  4
 7 hab_dcid_woods       0.336     0.0161     20.9  6.55e- 97
 8 hab_evgr_woods      -0.0797    0.0192     -4.15 3.36e-  5
 9 hab_mixed_woods      0.420     0.0158     26.5  3.17e-155
10 hab_orchard         -0.307     0.0252    -12.2  4.00e- 34
# … with 49 more rows

feeder_test_pred <- predict(feeder_fit, feeder_test, type = "prob") %>%
  mutate(.pred_class = as.factor(ifelse(.pred_squirrels >=0.5,
                                        "squirrels", "no squirrels"))) %>%
  bind_cols(feeder_test %>% select(squirrels))

feeder_train_pred

# A tibble: 176,763 × 4
   `.pred_no squirrels` .pred_squirrels .pred_class squirrels   
                  <dbl>           <dbl> <fct>       <fct>       
 1                0.168           0.832 squirrels   no squirrels
 2                0.168           0.832 squirrels   no squirrels
 3                0.358           0.642 squirrels   no squirrels
 4                0.166           0.834 squirrels   no squirrels
 5                0.274           0.726 squirrels   no squirrels
 6                0.191           0.809 squirrels   no squirrels
 7                0.288           0.712 squirrels   no squirrels
 8                0.184           0.816 squirrels   no squirrels
 9                0.227           0.773 squirrels   no squirrels
10                0.350           0.650 squirrels   no squirrels
# … with 176,753 more rows

rbind(accuracy(feeder_test_pred, truth = squirrels, estimate = .pred_class),
      sensitivity(feeder_test_pred, truth = squirrels, estimate = .pred_class),
      specificity(feeder_test_pred, truth = squirrels, estimate = .pred_class))

# A tibble: 3 × 3
  .metric     .estimator .estimate
  <chr>       <chr>          <dbl>
1 accuracy    binary        0.814 
2 sensitivity binary        0.0988
3 specificity binary        0.985

Cross Validation

Cross validation for model comparison (which model is best?)
Cross validation for model evaluation (what is the accuracy rate of the model?)

Competing models

we use the test data to assess how the model does. But we haven’t yet thought about how to use the data to build a particular model.
compare two different models to predict whether or not there are squirrels
- Model 1: removes the information about the habitat and about the trees and shrubs
- Model 2: removes the information about feeding the birds

feeder_rec1 <- recipe(squirrels ~ ., data = feeder_train) %>%
  # delete the habitat variables
  step_rm(contains("hab")) %>%
  # delete the tree/shrub info
  step_rm(contains("atleast")) %>%
  step_impute_mean(all_numeric_predictors()) %>%
  step_nzv(all_numeric_predictors())

feeder_rec2 <- recipe(squirrels ~ ., data = feeder_train) %>%
  # delete the variables on when the birds were fed
  step_rm(contains("fed")) %>%
  # delete the variables about the bird feeders
  step_rm(contains("feed")) %>%
  step_impute_mean(all_numeric_predictors()) %>%
  step_nzv(all_numeric_predictors())

How can we decide?

~~measure which model does better on the test data~~
~~measure which model does better on the training data~~
measure which model does better on the cross validated data

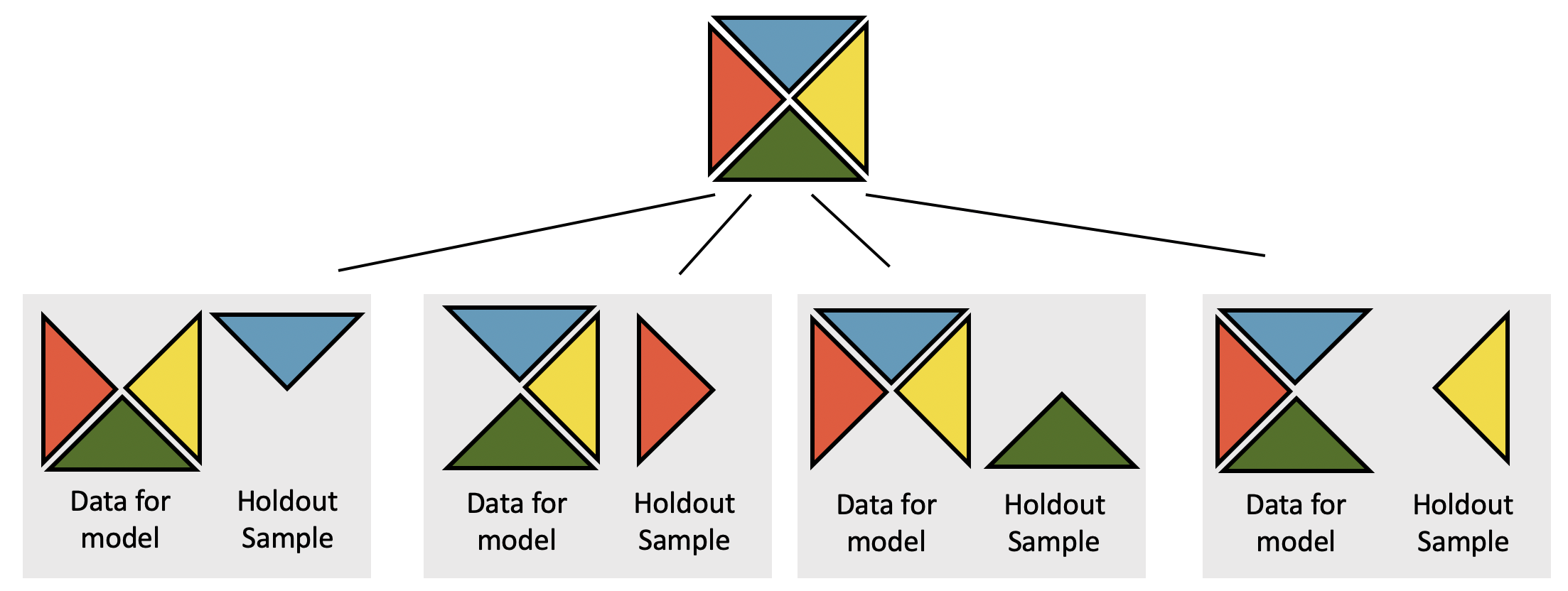
How does cross validation work?

4-fold CV is depicted. Notice that the holdout group is never used as part of the coefficient estimation process.

Cross validation

More specifically, v-fold cross validation:

Randomly partition the training data into v group
Use v-1 groups to build the model (calculate MLEs); use 1 group for prediction / assessment
Repeat v times, updating which group is used for assessment each time

Cross validation, step 1

Consider the example below where the training data are randomly split into 3 partitions:

Thirty observations are seen where three colors are used to demonstrate that the observations can be partitioned into three groups. — Splitting the data into a partition of v=3 groups. Source: (Kuhn and Silge 2022)

Cross validation, steps 2 and 3

Use 1 partition for assessment, and the remaining v-1 partitions for analysis
Repeat v times, updating which partition is used for assessment each time

Three iterations of model fitting are shown, each time using only 2/3 of the observations. The remaining 1/3 of the observations are used to estimate the performance of the model. — With the data split into three groups, we can see how 2/3 of the observations are used to fit the model and 1/3 of the observations are used to estimate the performance of the model. Source: (Kuhn and Silge 2022)

Cross validation using tidymodels

set.seed(4747)
folds <- vfold_cv(feeder_train, v = 3, strata = squirrels)
folds

#  3-fold cross-validation using stratification 
# A tibble: 3 × 2
  splits                 id   
  <list>                 <chr>
1 <split [117841/58922]> Fold1
2 <split [117842/58921]> Fold2
3 <split [117843/58920]> Fold3

Fit the model separately to each fold

feeder_rec1 <- recipe(squirrels ~ ., data = feeder_train) %>%
  # delete the habitat variables
  step_rm(contains("hab")) %>%
  # delete the tree/shrub info
  step_rm(contains("atleast")) %>%
  step_impute_mean(all_numeric_predictors()) %>%
  step_nzv(all_numeric_predictors())

feeder_rec1

Recipe

Inputs:

      role #variables
   outcome          1
 predictor         58

Operations:

Variables removed contains("hab")
Variables removed contains("atleast")
Mean imputation for all_numeric_predictors()
Sparse, unbalanced variable filter on all_numeric_predictors()

feeder_log <- logistic_reg() %>%
  set_engine("glm")

feeder_log

Logistic Regression Model Specification (classification)

Computational engine: glm

feeder_wflow1 <- workflow() %>%
  add_recipe(feeder_rec1) %>%
  add_model(feeder_log) 

feeder_wflow1

══ Workflow ════════════════════════════════════════════════════════════════════
Preprocessor: Recipe
Model: logistic_reg()

── Preprocessor ────────────────────────────────────────────────────────────────
4 Recipe Steps

• step_rm()
• step_rm()
• step_impute_mean()
• step_nzv()

── Model ───────────────────────────────────────────────────────────────────────
Logistic Regression Model Specification (classification)

Computational engine: glm

metrics_interest <- metric_set(accuracy, roc_auc, 
                              sensitivity, specificity)

feeder_fit_rs1 <- feeder_wflow1 %>%
  fit_resamples(resamples = folds,
                metrics = metrics_interest,
                control = control_resamples(save_pred = TRUE,
                                            event_level = "second"))

feeder_fit_rs1 %>% augment() %>%
  select(squirrels, .pred_class) %>%
  yardstick::conf_mat(squirrels, .pred_class) %>%
  autoplot(type = "heatmap") + 
  scale_fill_gradient(low="#D6EAF8", high="#2E86C1")

collect_metrics(feeder_fit_rs1)

# A tibble: 4 × 6
  .metric     .estimator   mean     n  std_err .config             
  <chr>       <chr>       <dbl> <int>    <dbl> <chr>               
1 accuracy    binary     0.809      3 0.000247 Preprocessor1_Model1
2 roc_auc     binary     0.663      3 0.00180  Preprocessor1_Model1
3 sensitivity binary     0.996      3 0.000190 Preprocessor1_Model1
4 specificity binary     0.0265     3 0.000545 Preprocessor1_Model1

Repeat the CV analysis for the second model

feeder_rec2 <- recipe(squirrels ~ ., data = feeder_train) %>%
  # delete the variables on when the birds were fed
  step_rm(contains("fed")) %>%
  # delete the variables about the bird feeders
  step_rm(contains("feed")) %>%
  step_impute_mean(all_numeric_predictors()) %>%
  step_nzv(all_numeric_predictors())

feeder_rec2

Recipe

Inputs:

      role #variables
   outcome          1
 predictor         58

Operations:

Variables removed contains("fed")
Variables removed contains("feed")
Mean imputation for all_numeric_predictors()
Sparse, unbalanced variable filter on all_numeric_predictors()

feeder_log <- logistic_reg() %>%
  set_engine("glm")

feeder_log

Logistic Regression Model Specification (classification)

Computational engine: glm

feeder_wflow2 <- workflow() %>%
  add_recipe(feeder_rec2) %>%
  add_model(feeder_log) 

feeder_wflow2

══ Workflow ════════════════════════════════════════════════════════════════════
Preprocessor: Recipe
Model: logistic_reg()

── Preprocessor ────────────────────────────────────────────────────────────────
4 Recipe Steps

• step_rm()
• step_rm()
• step_impute_mean()
• step_nzv()

── Model ───────────────────────────────────────────────────────────────────────
Logistic Regression Model Specification (classification)

Computational engine: glm

metrics_interest <- metric_set(accuracy, roc_auc, 
                              sensitivity, specificity)

feeder_fit_rs2 <- feeder_wflow2 %>%
  fit_resamples(resamples = folds,
                metrics = metrics_interest,
                control = control_resamples(save_pred = TRUE,
                                            event_level = "second"))

feeder_fit_rs2 %>% augment() %>%
  select(squirrels, .pred_class) %>%
  yardstick::conf_mat(squirrels, .pred_class) %>%
  autoplot(type = "heatmap") + 
  scale_fill_gradient(low="#D6EAF8", high="#2E86C1")

collect_metrics(feeder_fit_rs2)

# A tibble: 4 × 6
  .metric     .estimator   mean     n  std_err .config             
  <chr>       <chr>       <dbl> <int>    <dbl> <chr>               
1 accuracy    binary     0.813      3 0.000325 Preprocessor1_Model1
2 roc_auc     binary     0.698      3 0.00228  Preprocessor1_Model1
3 sensitivity binary     0.990      3 0.000424 Preprocessor1_Model1
4 specificity binary     0.0693     3 0.000291 Preprocessor1_Model1

Compare two models

Model 1

collect_metrics(feeder_fit_rs1)

# A tibble: 4 × 6
  .metric     .estimator   mean     n  std_err .config             
  <chr>       <chr>       <dbl> <int>    <dbl> <chr>               
1 accuracy    binary     0.809      3 0.000247 Preprocessor1_Model1
2 roc_auc     binary     0.663      3 0.00180  Preprocessor1_Model1
3 sensitivity binary     0.996      3 0.000190 Preprocessor1_Model1
4 specificity binary     0.0265     3 0.000545 Preprocessor1_Model1

Model 2

collect_metrics(feeder_fit_rs2)

# A tibble: 4 × 6
  .metric     .estimator   mean     n  std_err .config             
  <chr>       <chr>       <dbl> <int>    <dbl> <chr>               
1 accuracy    binary     0.813      3 0.000325 Preprocessor1_Model1
2 roc_auc     binary     0.698      3 0.00228  Preprocessor1_Model1
3 sensitivity binary     0.990      3 0.000424 Preprocessor1_Model1
4 specificity binary     0.0693     3 0.000291 Preprocessor1_Model1

Cross validation then test data

Nested cross-validation: two cross-validation loops are run one inside the other. (Varoquaux et al. 2017)

Bias-variance trade-off

Test and training error as a function of model complexity. Note that the error goes down monotonically only for the training data. Be careful not to overfit!! (Hastie, Tibshirani, and Friedman 2001)

References

Hastie, T., R. Tibshirani, and J. Friedman. 2001. The Elements of Statistical Learning. Springer.

Kuhn, Max, and Julia Silge. 2022. Tidy Modeling with r. https://www.tmwr.org/.

Varoquaux, G., P. Reddy Raamana, D. Engemann, A. Hoyos-Idrobo, Y. Schwartz, and B. Thirion. 2017. “Assessing and Tuning Brain Decoders: Cross-Validation, Caveats, and Guidelines.” NeuroImage 145: 166–79.

Reuse

https://creativecommons.org/licenses/by/4.0/

Other Formats

Agenda

Comparing Models

Data & goal

Feeders

Other variables

Modeling

Train / test

Training data

Feature engineering

Modeling workflow

Building recipes

Initiate a recipe

Working with recipes

Impute missing values & Remove zero variance predictors

Prep and bake

Building workflows

Specify model

Build workflow

View workflow

Fit model to training data

Model fit summary

All together

Evaluate model

Make predictions for training data

Accuracy

Visualizing accuracy

But, really…

Make predictions for testing data

Evaluate testing data

Evaluate testing data

Training vs. testing

What’s up with training data?

All together

Cross Validation

Competing models

Compare recipes

How can we decide?

How does cross validation work?

Cross validation

Cross validation, step 1

Cross validation, steps 2 and 3

Cross validation using tidymodels

Fit the model separately to each fold

Repeat the CV analysis for the second model

Compare two models

Model 1

Model 2

Cross validation then test data

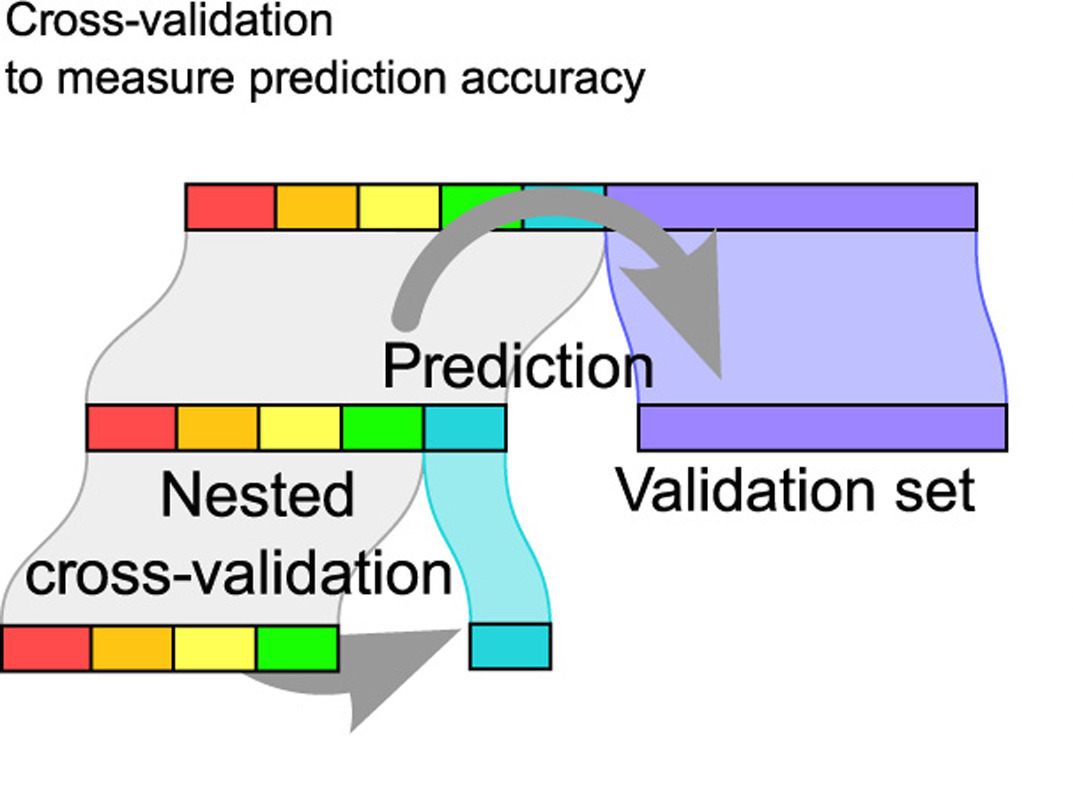
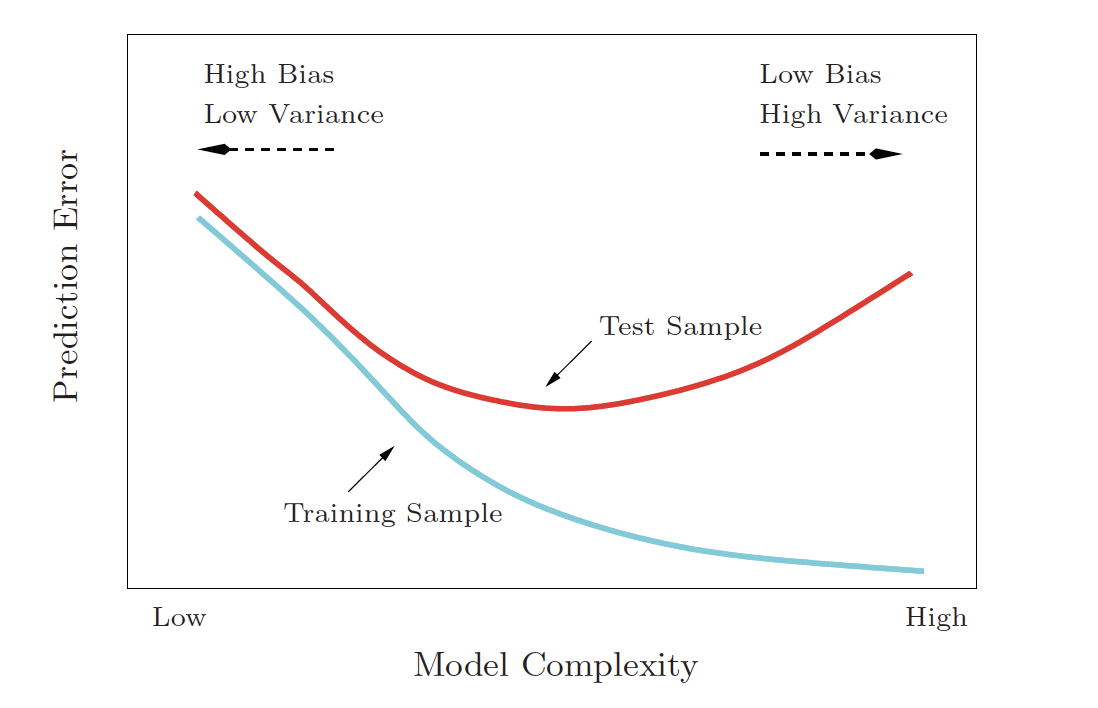
Bias-variance trade-off

References

Reuse